Это формула, представляющая выражение ( a + b ) n при положительном целом n в виде многочлена:
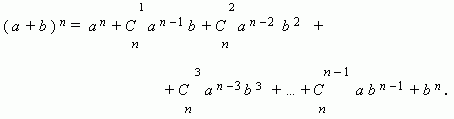
Или, по-другому, можем записать так: 
где п -показатель степени бинома, а член разложения 
стоит на (k+1) месте.
где п -показатель степени бинома, а член разложения стоит на (k+1) месте.
Заметим, что сумма показателей степеней для a и b постоянна и равна n.
Числа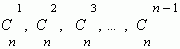 
называются биномиальными коэффициентами.
называются биномиальными коэффициентами.
Свойства сочетаний
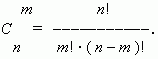
Из этой формулы ясно, что
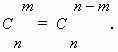
Заметим, что можно составить только одно сочетание из n элементов по n , которое содержит все nэлементов. Формула числа сочетаний даёт это значение, если только принять, что 0! = 1, что является определением 0! .
В соответствии с этим определением получим:
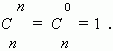
Общее число сочетаний можно вычислить, пользуясь и другим выражением:
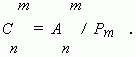
Биномиальные коэффициенты можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:
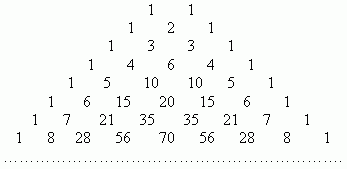
Первая строка в этой таблице содержит биномиальные коэффициенты для n = 1; вторая - для n = 2; третья - для n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение:
( a + b )7 ,
мы можем получить результат моментально, используя таблицу:
1. Сумма коэффициентов разложения ( a + b ) n равна 2 n .
2. Коэффициенты членов, равноудалённых от концов разложения, равны.
Это свойство следует из соотношения:
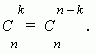
3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна
Домашнее задание по теме КОМБИНАТОРИКА. Срок выполнения 28.01.2015
Как обычно, ответы заносим в googleформу
Комментариев нет:
Отправить комментарий
Здесь можно оставить свои комментарии