 Домашнее задание по геометрии (тема "Объемы") смотри ЗДЕСЬ, в прежнем сообщении. Можно пойти по закладке В_9 и В_12, Д/З. Срок выполнения 04.02.2015. Удачи)))
Домашнее задание по геометрии (тема "Объемы") смотри ЗДЕСЬ, в прежнем сообщении. Можно пойти по закладке В_9 и В_12, Д/З. Срок выполнения 04.02.2015. Удачи)))Страницы
▼
воскресенье, 25 января 2015 г.
ДЗ по геометрии
 Домашнее задание по геометрии (тема "Объемы") смотри ЗДЕСЬ, в прежнем сообщении. Можно пойти по закладке В_9 и В_12, Д/З. Срок выполнения 04.02.2015. Удачи)))
Домашнее задание по геометрии (тема "Объемы") смотри ЗДЕСЬ, в прежнем сообщении. Можно пойти по закладке В_9 и В_12, Д/З. Срок выполнения 04.02.2015. Удачи)))пятница, 23 января 2015 г.
Комбинаторика,д/з
Это формула, представляющая выражение ( a + b ) n при положительном целом n в виде многочлена:
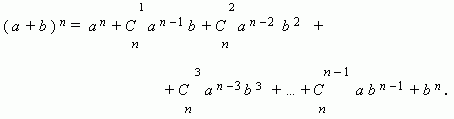
Или, по-другому, можем записать так:  где п -показатель степени бинома, а член разложения
где п -показатель степени бинома, а член разложения  стоит на (k+1) месте.
стоит на (k+1) месте.
 где п -показатель степени бинома, а член разложения
где п -показатель степени бинома, а член разложения  стоит на (k+1) месте.
стоит на (k+1) месте.
Заметим, что сумма показателей степеней для a и b постоянна и равна n.
Числа 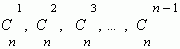 называются биномиальными коэффициентами.
называются биномиальными коэффициентами.
Свойства сочетаний
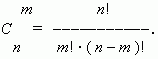
Из этой формулы ясно, что
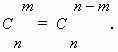
Заметим, что можно составить только одно сочетание из n элементов по n , которое содержит все nэлементов. Формула числа сочетаний даёт это значение, если только принять, что 0! = 1, что является определением 0! .
В соответствии с этим определением получим:
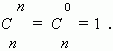
Общее число сочетаний можно вычислить, пользуясь и другим выражением:
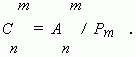
Биномиальные коэффициенты можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:
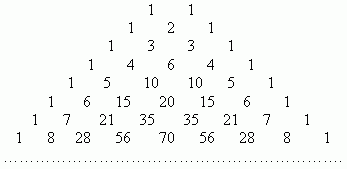
Первая строка в этой таблице содержит биномиальные коэффициенты для n = 1; вторая - для n = 2; третья - для n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение:
( a + b )7 ,
мы можем получить результат моментально, используя таблицу:
1. Сумма коэффициентов разложения ( a + b ) n равна 2 n .
2. Коэффициенты членов, равноудалённых от концов разложения, равны.
Это свойство следует из соотношения:
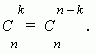
3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна
Домашнее задание по теме КОМБИНАТОРИКА. Срок выполнения 28.01.2015
Как обычно, ответы заносим в googleформу
четверг, 22 января 2015 г.
Олимпиады
Ребята!
Для тех, кто хочет участвовать в вузовских олимпиадах, сегодня публикую МИКС из заданий олимпиад экономических ВУЗов, в частности олимпиад, проводимых Высшей Школой Экономики. Некоторые задания мы с Вами разбирали на занятиях, другие ждут Вашего решения. Решайте, обсуждайте, спрашивайте... Можете сообщать мне Ваши идеи, решения, ответы в комментариях. Обратите внимание на задачу №9, уж очень часто ее условие повторяется в текстах олимпиад...
Задания ЗДЕСЬ .
А вот еще одна задачка, которая сначала мне показалась "странной"... Она была в тексте олимпиадных заданий под номером 1.
 Итак, ЗАДАЧА.
Итак, ЗАДАЧА.
В классе каждый мальчик дружит ровно с тремя девочками, а каждая девочка дружит ровно с двумя мальчиками. Известно, что в классе 12 парт, и за каждой партой сидит не более двух человек. Еще известно, что 16 детей в классе учится на "отлично". Сколько человек в классе?
Решили? Жду Ваших решений))))
Напоминаю Вам, что 30 января 2015 года будет проходить I тур олимпиада им. Н.Д. Кондратьева. Эта олимпиада входит в перчень олимпиад школьников, утверждаемый Министерством образования РФ, и, соответственно, повышает Ваши шансы при поступлении в ВУЗ. Если Вы хотите участвовать в нем, необходимо зарегистрироваться на сайте университета. Участникам олимпиады необходимо заполнить согласие законного представителя участника олимпиады на обработку персональных данных и заявку по установленной форме в бумажном и электронном виде http://olympias.ru/ostavit-zayavku/online-zayavka.
Для тех, кто хочет участвовать в вузовских олимпиадах, сегодня публикую МИКС из заданий олимпиад экономических ВУЗов, в частности олимпиад, проводимых Высшей Школой Экономики. Некоторые задания мы с Вами разбирали на занятиях, другие ждут Вашего решения. Решайте, обсуждайте, спрашивайте... Можете сообщать мне Ваши идеи, решения, ответы в комментариях. Обратите внимание на задачу №9, уж очень часто ее условие повторяется в текстах олимпиад...
Задания ЗДЕСЬ .
А вот еще одна задачка, которая сначала мне показалась "странной"... Она была в тексте олимпиадных заданий под номером 1.
В классе каждый мальчик дружит ровно с тремя девочками, а каждая девочка дружит ровно с двумя мальчиками. Известно, что в классе 12 парт, и за каждой партой сидит не более двух человек. Еще известно, что 16 детей в классе учится на "отлично". Сколько человек в классе?
Решили? Жду Ваших решений))))
Напоминаю Вам, что 30 января 2015 года будет проходить I тур олимпиада им. Н.Д. Кондратьева. Эта олимпиада входит в перчень олимпиад школьников, утверждаемый Министерством образования РФ, и, соответственно, повышает Ваши шансы при поступлении в ВУЗ. Если Вы хотите участвовать в нем, необходимо зарегистрироваться на сайте университета. Участникам олимпиады необходимо заполнить согласие законного представителя участника олимпиады на обработку персональных данных и заявку по установленной форме в бумажном и электронном виде http://olympias.ru/ostavit-zayavku/online-zayavka.
суббота, 17 января 2015 г.
Тренировочный вариант 81
Ребята!
Мы начинаем активно готовиться к написанию ЕГЭ. Для тренировки будем использовать различные материалы. К следующему уроку Вам было задано такое домашнее задание: прорешать ТРЕНИРОВОЧНЫЙ ВАРИАНТ №81, посмотреть, что вызывает затруднения, выяснить причину своих затруднений, ... Текст варианта №81 можно увидеть ЗДЕСЬ. Этот вариант опубликован на сайте http://alexlarin.net/ege/2015 в разделе ЕГЭ, материалы 2015 года. На этом же сайте опубликованы ответы к заданиям этого варианта, разбираются решения. По результатам решения теста попробуйте оценить себя сами, используя следующую таблицу:
На сайте http://alexlarin.net/ege/matem/main.html имеется генератор заданий ЕГЭ. Можете при подготовке воспользоваться и им. Не забываем, на следующем уроке будем писать тест уже в классе. Удачи!))
воскресенье, 11 января 2015 г.
В_9 и В_12, д/з


Ребята!

Вот мы и познакомились с формулами объема пирамиды и наклонной призмы. В экзаменационных вариантах ЕГЭ имеются задачи (В 12) по данной теме.
 Давайте проверим, как Вы умеете решать такие задачи. Воспользуемся сайтом, который создали добрые люди - http://egemaximum.ru/. Пройдите по ссылке и решите тест. Тест по пирамидам ЗДЕСЬ. На этом сайте также можно посмотреть, как решаются типовые задачи по этой и другим темам, проверить свое решение. Так что тренируемся. В скором времени - проверочная работа по этой теме. Удачи)))
Давайте проверим, как Вы умеете решать такие задачи. Воспользуемся сайтом, который создали добрые люди - http://egemaximum.ru/. Пройдите по ссылке и решите тест. Тест по пирамидам ЗДЕСЬ. На этом сайте также можно посмотреть, как решаются типовые задачи по этой и другим темам, проверить свое решение. Так что тренируемся. В скором времени - проверочная работа по этой теме. Удачи)))Срок выполнения Д/З - 26.01.2015. Удачи)))
Форма для занесения ответов:
25.01.2015
 Следующее домашнее задание по теме "Объемы" ЗДЕСЬ. Как всегда, решаем, результаты заносим в googleформу. Срок выполнения 04.02.2015.
Следующее домашнее задание по теме "Объемы" ЗДЕСЬ. Как всегда, решаем, результаты заносим в googleформу. Срок выполнения 04.02.2015.Сразу же скажем о планах на будущее: 02.02.2015 состоится урок, посвященный (ни много, ни мало!!!!) Архимеду. Готовьтесь)))
На нашем блоге размещены некоторые материалы об Архимеде, можно пройти по ссылке ЗДЕСЬ.
Форма для занесения ответов по ДОМАШНЕМУ ЗАДАНИЮ:
Про Архимеда
Дорогие ребята!
В скором времени у нас состоится урок-занятие, посвященное Архимеду.
В качестве анонса к мероприятию, давайте поговорим об Архимеде, о его жизни, о его изобретениях и открытиях...
По признанию ученых Архимед – один из выдающихся деятелей науки, чье творчество имело величайшее значение для нашей цивилизации
А вот полезный мультик, который в популярной форме рассказывает об Архимеде.
До наших дней дошло совсем немного трактатов Архимеда (всего 13). И вот в начале 20-го века был обнаружен палимпсест Архимеда. Эта книга содержала тексты Архимеда,записанные в Византии в X веке. В XIII веке поверх текстов Архимеда были записаны христианские тексты. Вот ссылка из Википедии, рассказывающая об этой рукописи, - ЗДЕСЬ. Сейчас палимпсест интенсивно исследуется. В следующем фильме идет речь о судьбе палимпсеста и о том, как его расшифровывают. Знакомьтесь, удивляйтесь, поражайтесь)))
В скором времени у нас состоится урок-занятие, посвященное Архимеду.
В качестве анонса к мероприятию, давайте поговорим об Архимеде, о его жизни, о его изобретениях и открытиях...
По признанию ученых Архимед – один из выдающихся деятелей науки, чье творчество имело величайшее значение для нашей цивилизации
Биографические сведения об Архимеде крайне скудны. Известно, что он был сыном астронома и математика Фидия. Учился и некоторое время работал в Александрии (Египет). Архимеда всю жизнь связывали дружеские отношения с тамошними учеными (Эратосфеном, Кононом, Досифеем), и многие его труды сохранились благодаря переписке с ними. Затем Архимед возвращается в Сиракузы, где свыше 25 лет отдает научной и инженерно-изобретательской работе, работая и главным инженером-теоретиком, и исполнителем широких оборонительных работ. На это время приходятся самые выдающиеся его открытия.
Посмотрите небольшое видео об Архимеде.
До наших дней дошло совсем немного трактатов Архимеда (всего 13). И вот в начале 20-го века был обнаружен палимпсест Архимеда. Эта книга содержала тексты Архимеда,записанные в Византии в X веке. В XIII веке поверх текстов Архимеда были записаны христианские тексты. Вот ссылка из Википедии, рассказывающая об этой рукописи, - ЗДЕСЬ. Сейчас палимпсест интенсивно исследуется. В следующем фильме идет речь о судьбе палимпсеста и о том, как его расшифровывают. Знакомьтесь, удивляйтесь, поражайтесь)))






