Очень тяжело у нас идут задачи по геометрии.
Для устранения этой проблемы следует
1. хорошо выучить теорию;
2. научиться строить чертежи;
3. применять имеющиеся знания к решению задач.
Поэтому сегодня мы еще раз разберем пошагово некоторые задачи. Это Д/З: разобрать, закончить решение, записать в тетрадь.
ЗАДАЧА №1.
Точка М одинаково удалена от
вершин равностороннего треугольника АВС,
сторона которого равна а. Расстояние от точки М до
плоскости треугольника равно а. Вычислите угол между:
1. прямой МА и плоскостью треугольника АВС;
2. прямой МЕ (Е – середина ВС) и
плоскостью треугольника АВС.
УКАЗАНИЯ к
решению.
Первое, что
следует отметить, анализируя условие, что точка М проецируется в центр
описанной окружности ΔАВС, т.к. … (продолжите самостоятельно). Т.о. точка О ,
центр описанной окружности около правильного ΔАВС, лежит на высоте (медиане) АЕ
и делит ее в отношении 2:1, считая от вершины. Сделаем чертеж.
Далее давайте определим, какие углы нам следует найти.
1.
Угол между прямой МА и плоскостью
треугольника АВС. По определению, угол между прямой и плоскостью – это угол
между прямой и ее проекцией на эту плоскость. Т.е. в нашем случае: ОМ⊥(АВС); АМ - наклонная, ОА – ее проекция, значит
искомый угол - ∟МОА. Этот угол можно найти, рассматривая ΔМОА. Далее решайте самостоятельно.
2.
Угол между прямой МЕ (Е – середина ВС) и плоскостью треугольника АВС.
Заполните пропуски: ОМ⊥(АВС); МЕ – наклонная, …. - проекция, значит искомый угол - ∟…
ЗАДАЧА №2
Через сторону АВ прямоугольника
АВСD
проведена плоскость α.
Сторона СD
удалена от этой плоскости на 3 см, СВ=6см, DС=8см. вычислите:
1. угол
между прямой DА
и плоскостью α;
2. синус
угла между прямой ВD
и плоскостью α.
Давайте
сделаем чертеж к задаче.
Построим плоскость α. Пусть в нашем случае DМ⊥α; СР⊥α.
Ответьте на вопросы:
1. Почему прямые РС и DM определяют
плоскость? (Как они расположены друг относительно друга?)
2.
Каково
взаимное расположение прямой АВ и плоскости (МРС), почему?
3.
Укажите
проекцию прямой DМ
на плоскость α. Как расположена эта проекция относительно прямой АВ? Найдите
угол между этими прямыми.
4.
Укажите
на чертеже угол между прямой DА
и плоскостью α.
Из какого треугольника будете находить этот угол?
5.
Укажите
на чертеже угол между прямой DВ
и плоскостью α.
Из какого треугольника будете находить этот угол?
ЗАДАЧА №3
Катет прямоугольного треугольника
АВС лежит в плоскости α.
Вершина А удалена от нее на
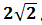 дм. ВС=АС=4 дм. Вычислите угол между плоскостью α и прямой
дм. ВС=АС=4 дм. Вычислите угол между плоскостью α и прямой
1) АС;
2) АВ.
На
чертеже АН⊥α.
В ΔАВС
АВ – катет, а где гипотенуза? Найдите ее.
Далее
работаем по известной схеме:
находим перпендикуляр к плоскости,
наклонную,
ее
проекцию,
угол между прямой и плоскостью.
ЗАДАЧА №4
Плоскости
прямоугольных треугольников АВС и АВК перпендикулярны. АВ=6, АК=8, ∟АВК=∟АВС=90⁰,
∟ВАС=45⁰. Вычислите расстояние между:
1. точками
К и С;
2. прямыми
ВК и АС.
 Учитывая,
что плоскости прямоугольных треугольников АВС и АВК перпендикулярны, а
углы ∟АВК=∟АВС=90
Учитывая,
что плоскости прямоугольных треугольников АВС и АВК перпендикулярны, а
углы ∟АВК=∟АВС=90⁰
, отредактируем чертеж:
Подумайте,
какой отрезок будет являться расстоянием между прямыми АС и КВ? Найдите его.
Дополнительный вопрос: укажите
линейный угол двугранного угла КВАС.
 Прямая и наклонная призмы
Прямая и наклонная призмы Прямая и наклонная призмы
Прямая и наклонная призмы