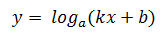Дорогие ребята! Сегодня поговорим о выпуклости и вогнутости графиков функций. Для начала немного теории.
Определение
Дифференцируемая функция называется выпуклой вниз на интервале (a;b), если ее график расположен не ниже касательной к нему в любой точке интервала (a;b).
И аналогично:
Дифференцируемая функция называется выпуклой вверх на интервале (a;b), если ее график расположен не выше касательной к нему в любой точке интервала (a;b).
За выпуклость или вогнутость графиков функций "отвечает" вторая производная.
Кроме этого, нам известна выпуклость или вогнутость элементарных функций, таких как квадратичная функция, различные виды степенных функций, логарифмическая и показательная функции и др.
Выпуклость и вогнутость их мы теперь можем обосновать с помощью теорем, находя вторую производную (см. выше).
1. К тому же мы можем говорить о выпуклости (вогнутости) суммы выпуклых или вогнутых функций. Т.е. верна такая теорема, если графики функций f(x) и g(x) выпуклы вверх, то и их сумма f(x) + g(x) будет иметь выпуклость вверх на пересечении областей определения этих функций.
2. Кроме того, мы можем использовать знания по преобразованию графиков. Например, верно такое утверждение: если график функции f(x) выпукл вверх, то функция "- f(x)" будет иметь выпуклость вниз.
Примеры

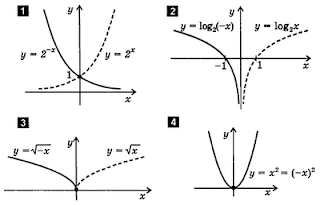
На следующем рисунке представлено, каким образом из графика функции у=f(x) получить график функции у=f(-x). Подумайте, меняется ли при этом преобразовании выпуклость графика?
Для нас представляет интерес, как можно использовать данное свойство при решении задач, уравнений. Сегодня рассмотрим уравнение, которое было предложено
учителям на 8-ой олимпиаде Эйлера, организуемой Фондом Эйлера и школой при СПбГУ "УниШанс".
Решить это уравнение "стандартными" способами весьма затруднительно. Попробуйте))) А вот, используя свойство выпуклости графиков
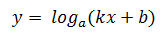
легко и просто.
Ниже представлено решение этого уравнения двумя способами.
А теперь я Вам предлагаю поупражняться в составлении таких уравнений ("за отдельную плату"). Вам нужно в открытой для Вас Google-презентации оформить 3 уравнения, представить их решение. Редактировать эту презентацию смогут те ребята, кто имеет доступ редактора. Если у Вас такого нет, запросите у меня доступ. Читать презентацию смогут все (общедоступно в Интернете). Не забудьте указать свою фамилию)) В добрый путь, удачи!
ПРЕЗЕНТАЦИЯ ЗДЕСЬ